世の中は誤解にみちている～モンティホール問題　

高校数学も分からない輩の戯言ですので華麗にスルーお願いします。

※追記
NHKの数学Ⅰでもモンティホール問題が紹介されていたので改めて（個人的に考えた）まとめておくと、
なぜその箱なりドアをあけるのか？
残った箱、ドアをなぜあけないのか？
これは確率というよりロジックの話である

結論　残された箱に変更したほうが当たる確率が上がるというのはミスリードである

モンティホール問題は史上最もIQの高い女性と言われるマリリンヴォスサヴァントが、「残された箱に変更したほうがいい」と言ったことにより論争に火がついた。
なぜなら一般人のみならず数学者であっても、選択を変えようが変えまいが当たる確率は半々で変わらないと考えたからである。
しかし、コンピューターシミュレーションの結果は残された箱に変更したほうが当たる確率は倍になるという結果が得られた。
なぜ数学者であっても確率は半々だと結論付けるのか？これがこの問題の最大の疑問点であるが、結論としては

司会者が選択する前と後の当たる確率を混同しているからである。参加者が選択した箱をそのままにすると、司会者が何を選ぼうが当たる確率は3分の1であるが、司会者が選択した後は、司会者の箱が1個除外されるので当たる確率は2分の1になる。そして残された箱が当たる確率も2分の1になる。
これは司会者が箱を開けた状態＝箱を除外した場合の当たる確率であるが、賞金や商品を当てたい参加者が知りたいのは元々の選択肢ABC3つの箱に対してどれくらいの確率になるか？ということである。司会者が箱を除外しなければ残りの箱に変更しようがしまいが当たる確率は3分の1で変わらない。
1個除外されたことにより残された箱に変更したほうが当たる確率が高くなるのは当たる確率が上昇するという意味ではなく、そのままを選択し続けると当たる確率は変わらないと解釈すべきである。
従って、それ自体は間違いではない。しかし、ここで問題にされているのは、「そのままor変更」であり、必ずしもAやBが当たる確率ではない。
そして、それが各当たり、A、B、Cの３種類で行われる。ABCの当たりをランダムに100回くらい抽選を行った場合、司会者が何を選ぼうがずっとAだけを選び続けていたら当たる確率は3分の1である。
仮に、司会者が何も箱を開けずに参加者に変更だけを許した場合、変更した場合の当たる確率はどうなるだろうか？つまり、箱は除外されない場合である。

この点、後に見るようにモンティホール問題の解説でみられる残された箱のグループが3分の2なのでそもそもそのグループに属しているものを選ぶから当たる確率が高いのだという解釈は間違いである。

当たりがAでAを最初選択し、Bに変更しようがCに変更しようがそれは変更の範疇であるがこの場合は絶対に当たらない
当たりがAでBを最初選択し、Aに変更しようがCに変更しようがそれは変更の範疇であるがこの場合は当たる可能性があるが必ず当たるわけではない
当たりがAでCを最初選択し、Aに変更しようがBに変更しようがそれは変更の範疇であるがこの場合は当たる可能性があるが必ず当たるわけではない

要するに残された箱が1個に限定されず2個あるので、選択肢が各回で2個ずつあり、全部で6つの選択肢があることになる。
このうち当たるのは２つしかないので当たる可能性は3分の1である。

命題としては「参加者は選択を変えないほうがいいのか？それとも選択を変えたほうがいいのか？」言い換えればどちらが当たる確率が高いのかである。
この点につきよく見られるのは、残された箱のグループのほうが参加者が選択した箱よりそもそも確率が高いという説明であるがこれも問題の本質をミスリードしている。
選択を変えると当たる確率が上がるわけではないし、選択を変えなければ必ず当たるわけでもない。
そして、重要な点は変えようが変えまいが当たる確率は半々であると考えた数学者も一般人も決して間違いではないという点である。
後に見るように実は選択を変えようが変えまいが当たる確率は半々であるが、これは司会者が箱をあけた以降の当たる確率の話である。当たるか当たらないかで言い始めると半々になるのは自明。
モンティホール問題のキモはそのままの場合の的中率と変更した場合の的中率はどちらが高いかである。選択後に的中率が上がる、という話ではない。
普通に考えるとどうやっても確率半々になりそうであるが、
たまたまによれば、コンピューターシミュレーションにより、そのままの場合と変更した場合は１：２で変更したほうが当たる結果が出たそうである。
つまり、以前書いたような総当たり方式そのものが間違っているということになる。

目的は選んだ箱が当たるかどうかであるから
Aが当たり
Bが当たり
Cが当たり
の3パターンがある。

数学者でも陥るモンティホール問題の解き方

これが各1回（確率で言えば分母になる）で、参加者が選択後司会者が選択、そしてそのままだと当たるのか変更すると当たるのか？という話である。

まず参加者が選択し、次に司会者が選択。これがセットで、そのままにしておくのか？残りに変更するのか？なので8パターンではなく６パターンになるようだ。
パターン１　Aが当たりの場合
参加者がAを選択後司会者がBCいずれを選んでもそのままであれば当たりになるが、2回当たりとしてカウントするのではなくそのままで当たり、変更すると外れ。
パターン２　Bが当たりの場合
参加者がAを選択後司会者はCしか選べず、そのままなら外れ、変更すれば当たりとなる
パターン３　Cが当たりの場合
参加者がAを選択後司会者はBしか選べず、そのままなら外れ、変更すれば当たりとなる

選択を2回しているが、選択を2回として×３ゲームにすると６回になるが、実際のゲームでは1回1選択しかできないので1回を選択として分母にする必要があるようだ。
この時、ほとんどの人がパターン１の場合に選択は2回で、そのままにしておくと当たりが2回となり、変更も2回で外れ2回とカウントしているようだ。
そして、パターン２と３はそのまま1回ずつ変更も1回ずつで、そのままの場合の分母が合計4回、変更の場合の分母が合計4回としてしまう。

司会者が選択した箱以外の当たる確率を算出する

例えば宝くじで言えばくじ券は言わば選択肢である。当たりが1本でくじ券が100枚なら当たる確率は当然100分の1となる。
くじ券は選択肢であり抽選は1回、当たりは1個である。
くじ券が各1回ずつ当たるようにすると、100回抽選を行えば必ず各くじ券1回当たることになるが、1回の抽選で当たる確率は100分の1で変わらない。
モンティホール問題でも同じように考えると、くじ券は各選択肢ということになるので当たりの確率を調べるには全選択肢が分母となる。
パターン１の場合の選択肢は　①そのまま　②Bに変更　③Cに変更の　３つ
パターン２の場合は　①そのまま　②Bに変更　の２つ
パターン３の場合　①そのまま　②Cに変更　の２つ
合計７つの選択肢があり、そのままにした場合は１つしか当たらず変更した場合は２つ当たる
そうすると確率は7分の１と7分の２となるが、実際にそのままを選択し続けると当たる確率は3分の1であり変更を選択し続けると当たる確率は3分の2となｒ。
つまり、この問題は単純な確率の話（そのままを選択し続ける）と、司会者が選択した以外の箱の当たりの確率の話である。
司会者が選択する箱は絶対に当たりではない。なぜなら彼は当たりを知っているからである。
従って、残された箱が当たりの確率は2分の1であるというのは間違いではない。
そして、参加者が選択した箱を変更せずそのままにし続けた場合当たる確率は3分の1である。司会者がどの箱を選択しようが、参加者がそのままを選択し続けると3分の1は変わらない。
この点、モンティホール問題の解釈説明では変更したほうがあたる確率が上がると説明されるため、まるで確率が変動しているかのように考えがちだが、実際は確率自体は変動していない。なぜなら当たりの箱が変動するわけではないからである。

参加者の選択した箱そのまま　VS　残された箱　

どちらがより当たるのか？という比較である。司会者は絶対に当たりの箱は開けない。そうすると残された箱か参加者の選択した箱が当たりなので当たりの確率は2分の1となる、というのは宝くじで言えば1回の抽選で当たる確率のことを言っている。重要なのは３つの箱があるのに司会者が1個選択してしまうと、当たる確率が2分の1になる点である。そうすると確かに元々3分の1の確率だったものが2分の1に上昇しているように見えるが、1個除外されているので当たり前であり、この場合の当たる確率は全体での当たる確率であり、残された箱の当たる確率ではない。残された箱の当たる確率及びそのままの箱の当たる確率は３つのパターンを分母として計算する必要がある。

パターン１の場合選択肢は３つあるが、1回の抽選で販売されるくじ券は１そのままの箱と２残された箱の2枚であり、BとCの2枚が販売されるわけではない（両方は選択できない）
また、そうすると結局当たる確率は2分の1になるが、これは１パターン毎の当たる確率であって、残された箱及びそのままの箱の当たる確率ではない。

そして、論点は「そのまま」と「変更」どちらが当たる確率が高いのかであり、当たる確率そのものを求めようとするものではない。
よって、コンピューターシミュレーションでも「１：２」という表現がされている。

そもそも当たるか当たらないかだと2分の1になるのは自明である。これは上記本にも書いてあり、要は分母になるものがなんなのかという点にある。
そのままor変更で当たるか外れるかなので、そのままを続けた場合に当たる確率、変更を続けた場合に当たる確率としなければならない。
また参加者選択、司会者選択後のそのまま、変更を各1回としてカウントするのではなく、1ゲームとしてカウントしなければならない。
言い換えると当たりがABCのいずれか1個に決定するのが1ゲームとなり、そのパターンは当たりがABCの3パターンとなる。
そして、選択をそのままにする場合と、変更する場合を比較するには各ゲーム＝パターンでそれをやり続けた結果を比較しなければならない。

また、「そのまま」だと当たる確率3分の1で、「変更する」と当たる確率は3分の2という説明もあるが、この部分が余計にミスリードを誘っているようだ。
しかし、これだと変更した箱の当たる額率が3分の2になるように見えるがそうではなく、変更した場合それぞれをひっくるめて3分の2だと言っているに過ぎない。
そして、この説明で元々Ａは3分の1で、ＢＣは3分の2だから、残されたほうを選択した方が確率が高いという。しかし、これも混乱のもとのような気がする。
元々BCを合わせて3分の2は当たり前の話なのに変更したほうが確率が高くなるというような珍妙な説明になってしまう。司会者の選択後に変更しようがしまいがそもそも確率は変わっていない。３つある箱でまず1個選択し、司会者が1個選択する。そして残された箱と元々選んでいた箱でどちらが当たる確率が高いのかという話である。

そうすると、当たりがランダムな場合、そのままを300ゲームくらいこなした場合と、残りの箱に変更をし続けた場合は変更し続けたほうがそのままの場合より2倍程度あたりがでることになる。

言い換えると、パターン１はそのままだと的中率100パーセントだがパターン２、３のときそのままだと100パーセント外れる。変更するとパターン1だと的中率ゼロパーセントだが、パターン２、３の場合に変更すると100パーセント的中することになる。
この結果を相対的にみると、確かに変更したほうが長い目でみると当たる確率は高くなる。
もっとも、テレビ番組のような1発勝負ではそんな大数の法則のようなものはほとんど意味のない机上の空論かもしれないが。

なぜ数学者でもモンティホール問題を間違うのか？

既に答えが出ているが、変更しようがしまいが実は確率に変化はない。司会者が選択すると残された箱の当たる確率が計算上上昇しているように見えるだけである。
AとB,Cというグループに分けると当たる確率が3分の1と3分の2であり、これは司会者の選択前と選択後で実は変化がない。
従って、数学者であっても変更しようがしまいが確率は変わらないという結論になり、確かに変わりはないが、そもそも論として参加者が選択した箱と、それ以外のグループに分けたらそれ以外のグループの当たる確率は3分の2である。司会者が何を選択しようがいずれにしろ残された箱はそれ以外のグループに所属しているのでそれ以外のグループを選択し続けると当たる確率は3分の2となる。
しかし、これは確率が上がったわけではない。

 

モンティホール問題の解説に対する疑問

A,B,Cの3つの箱のうちの一つに賞金が入っている。それを当てたら賞金が貰える。
あなたはAを選択。
答えを知っている司会者がCの箱を開けて中身が空だと見せる。
そしてあなたに言う「変更してもいいですよ」
さて、あなたはBに変更したほうがいいだろうか？
答えは変更した方がいいということになっている。

端的に言えば、答えを知っている司会者はBに入っているならCしか選ばないからだという。
ここで素朴な疑問がわく。
仮にAに入っているとするなら司会者はBとCどちらを選択しても同じである。
つまり、Cが開けられたからと言ってBに入っているとは限らない。
Bに入っていれば100％Cを開ける。これはBに入っていればという前提条件があってはじめて成り立つ論理である。
Aに賞金が入っている場合でもCを開ける可能性はある。その可能性は50％。
それに比べてBに賞金が入っている場合はCを開ける可能性は100％となる。
ということでBに入っている確率のほうが高いというロジックがこの３つの箱の問題のキモである。
勘違いしてはいけないのはBに入っている確率が100％とは言っていない点である。
Bに賞金が入っているという条件で考えるとCを開ける確率が100％になるというだけである。
この点、この問題に対する解説にあたかもCが開けられたことによりBに入っている確率が高くなるなどというものがあるが、確率自体が高くなるのだろうか？
確かに1/3から1/2にあがるかもしれないが、だからといってAよりもBに入っている確率が高くなるわけではない。
この点、もともとBに入っている確率は1/3だったものが1/2にあがったとも言えるが、それはAにも言えることである。
この問題はベイズ推定とも関係があるという言うが。

※追記　残された箱に変更し続けると本当に的中確率は上がるのか？

ベイズ推定という名の通り、これは言わば推論的確率と言っていいだろう。
Bに入っている確率が100％と聞くとまるで確実にBに入っているように思えるが、そうではなく、「Bに入っているとしたらCを開ける確率が100％」である。
通常の確率では当たる確率だが、ここで言っている確率は「それが当たるとしたらどれを選ぶか」その確率を言っているだけである。
従って、このモンティホール問題での解答である「変更したほうがいい」というのは本当だろうか。
仮にこの推定が正しいとするなら、同じように回答者が選択したもの以外で司会者が外れを開けていくことを繰り返す。回答者が変更する場合と変更しない場合の的中確率を比べると圧倒的に変更したほうの的中率が変更しない場合よりも上回るだろう（単純計算で2倍か？）
しかし、Cが開けられた時点で選択肢の一つが排除され当たる確率が2分の1になるだけとも言えるが、このモンティホール問題の推定ロジックでは残された箱に入っている確率が高くなることになる。
司会者は答えを知っていることが前提であるが、回答者が選んだAの箱が的中の場合に司会者がCを選ぶ可能性もある。このときはAに入っているという条件は確定済みである。そこで司会者がBを選ぶ可能性もあるが、仮にCを開けると客観的にはAかBに入っているからCを開けたとも言える。Bに入っているから必然的にCを選択したことにはならないが、Bに入っていることを知っていたら確実にCを選択しなければならない。もしも司会者が何も知らなければBを選択するのは2分の1だが答えを知っているので必ず2分の1とはならない。つまり司会者が答えを知っているという事前情報が必要であり、それが条件でもある。その条件があるならばそういう行動をとるだろうということになる。
もしも司会者が答えをしらなければそもそもこの推定は成り立たない。
とは言え、Ｂを選んだから確実にＡに入っているわけではなく、Ａを選んだからといって確実にＢに入っているわけではないという事実は変わらない。

残された箱に変更した場合とそのままにした場合

Ａが当たり　

Ａ●　解答者Ａ選択
Ｂ〇　司会者Ｂを開ける
Ｃ〇

解答者そのまま　→的中
解答者Ｃに変更　→外れ

Ａが当たり　

Ａ●　解答者Ａ選択
Ｂ〇
Ｃ〇　司会者Ｃを開ける

解答者そのまま　→的中
解答者Ｂに変更　→外れ

Ａが当たり　

Ａ●
Ｂ〇　解答者Ｂ選択
Ｃ〇　司会者Ｃを開ける

解答者そのまま　→外れ
解答者Ａに変更　→的中

Ａが当たり　

Ａ●
Ｂ〇　司会者Bを開ける
Ｃ〇　解答者C選択

解答者そのまま　→外れ
解答者Ａに変更　→的中

8パターンがあるが回答者が変更せずそのままを選択し続けると的中率4分の1となり、残された箱に変更し続けると的中率は4分の１となるが。。。

司会者がBを開けるのは2回この時、残された箱に変更すると的中2分の1
司会者がCを開けるのは2回この時、残された箱に変更すると的中2分の1
司会者がどの箱をあけようが解答者はそのままを選択してもやはり2分の１となる

モンティホール問題のロジックで言えば残された箱に変更し続けた方が的中率はそのままよりも上がるはずであるが。。。
この総当たり方式も考え方によって違いがでる

確率とデタラメの世界には確率のパラドックスの例として確率が変わるという点について言及した部分がある。看守のパラドックスという似たような話がでてくるが、アレンジされて色々と手を変え品を変え同じような問題が作り出されているようだ。
気をつけなければいけないのは問題の出し方や条件設定が少しでも違えばまったく違う話になる点であるが、それらが混同されて説明されている場合が多々ある。
間違いではないにしろミスリードと言っていいかもしれない。
そしてやはりこのモンティホール問題の解が腑に落ちない人が多数いるもよう。

結論としては
「よって、挑戦者がドアを替えない場合、当るのは①の場合だけ。確率は３分の１。
　ドアを替える場合、当るのは②と③の場合。つまり３分の２の確率で当ります。」
とある。確かこれと同じような説明が人生と投資のパズルにあった。
しかし、これは言わば当たり前のことである。３個あるものを２個と１個に分ければ当然そうなるが、確率が上がっているわけではない。残りの２個のうち１個が当たる確率は全体から見れば３分の１であり、３分の２というより２個のうちの１個なら２分の１になるのは当然である。
要は前提条件が変わっている、あるいは条件が追加されているとも言える。しかし、本当に確率が変わっているのかと言えるのか？
確率とデタラメの世界
あなたは新しく友達になった女性に子供がいるかどうか尋ねる
ええ二人いますと彼女は答える
女の子はいますか、とあなた
ええ、と彼女
このとき子供が二人とも女の子である確率は３分の１
女女
女男
男男
男女
※男男はありえない

問い方を変えてみる
上の子が女の子である場合二人とも女の子である確率は２分の１

元々の確率は４分の１であるが条件が変われば確率も変わる。
しかし、下の子供が女の子であるという事実は条件が変わっても変わらない。数学的には確率が変わるが、そこにある事実は変わらない。
確率というのはあくまで結果が分からない時点での話である。

要するに数学的にそうなる、という話と
現実との間に齟齬があるため腑に落ちない人がたくさんでてくるのだろう
数学的にそうなるという検証は散見されるが、実際に残された選択肢に変更したほうがそのままよりも的中率が高くなるという検証結果は見つけることができない

モンティホール問題とベルトランの箱問題にみえるパラドックス

モンティホール問題は元々
ニューヨークタイムズの数学 ～ モンティ・ホール問題 ～ ベルトランの箱のパラドクス
を下敷きにしているらしいが、確かにパラドックスである。

１枚取り出してそれが金貨
箱はSSかGSとなる
残された枚数が３枚となりうち２枚が金貨なので３分の２と考えることができるが、これもあくまで数学的計算であろう。
実際に箱を選ぶことを考えると１枚目が仮に金貨だったとしてその箱のもう１枚が銀貨から金貨に変化するわけもない。
仮にここで司会者がいてGGを開けた場合、残された箱に変更したほうが金貨２枚である確率が高くなるのがモンティホール問題であり、ベルトランの箱はそのままのほうが確率があがるという。
箱に入っているのが２つであり条件が違うと思われそうだが実際は同じと言っていい。

 

ベイズ推定について

ベイズ推定について勉強しようとアマゾンで検索していたら、本のレビューにこんな記述があった。
図解・ベイズ統計「超」入門 あいまいなデータから未来を予測する技術

論理を考えるときには、時間軸が重要。「叱られなければ勉強しない」の対偶（対偶は常に真）は「勉強すれば叱られる」で、一見おかしい。これは「（現在）勉強しているのは（過去に）叱られたから」と解釈する。

命題が真ならば対偶にしても真になるはずだがおかしい。
そもそも命題が真ではないのではないか？

 

叱られなければ　勉強しない
言い換えると　叱られると　勉強する
これを対偶にすると
勉強しない　叱られない　となりやはりおかしい
しかし、よくよく考えると叱られると勉強するということは勉強している時は叱られないのか？というと勉強している時でも叱られている時がある。
それは勉強以外の理由だろう。勿論ここで違う条件を出したらだめではないか？ということでこれは除外しよう。
いずれにしても叱られると勉強はする。
すると勉強しているときは叱られていないことになる。つまり叱られていないならば勉強しているということになる。
この対偶をとる。
勉強しない　叱られる　ということで　成立する。
しかし、叱られていないときは常に勉強しているかというと、そんなことはない。
また、勉強をしていないから叱られているのだが、勉強以外の理由で叱られることもあり得る。
他の条件を付加するというよりも様々な理由で叱られることがあり、叱られるその都度勉強をするわけではない。
つまり、やはりこの命題自体が真とは言えないということだろう。

ベイズ推定のロジック

ベイズ推定あるいはそれを公式化したものの考え方は、要するに我々が日頃様々なものについて予測や推測などをしていることを数値化するための道具であると言える。
従って、ベイズの定理を使えばあたかもなんでも推定できるように考えるのは危険だ。
迷惑メールのフィルターにベイズ推定が使われているのは有名だが、迷惑でないものが多数ゴミ箱に入れられていることからもそれは分かる。
要するに事前データによる確率が精度が高ければベイズ推定も当然よく機能する。ベイズ推定が一部もてはやされているのは結局のところ事前データにあまり信頼性がない場合でも使えるからだ。
とは言え、いずれにしろ公式化されていればそのロジック、考え方を様々な場面で応用できるということでもあり、もてはやされるのも頷ける。
プログラムやAIなどで使用する場合に重宝するからに他ならず、ベイズ推定だから確度が高くなるというわけではない。
この点を結構見落としがちである。

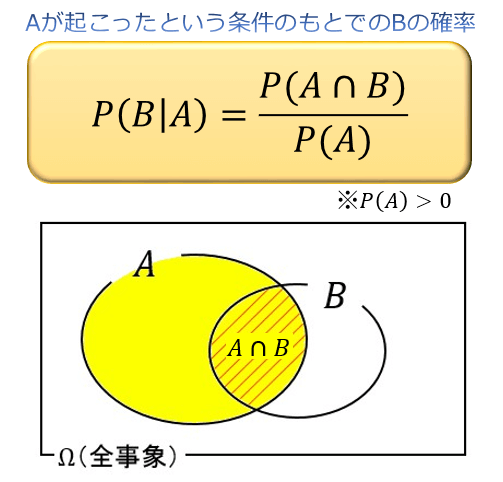
原因 → 結果 が分かっているときに 結果が起こったときの原因の確率を求める 数学の定理

乗法定理についての誤解

ベイズの定理とは何か。条件付き確率からわかる判別の知恵

例題）サイコロを振って偶数の目が出た場合に、それが4以上の目である確率は？

偶数の出る確率は2/1
4以上の出る確率で間違ってしまう。
偶数が出たなかで4以上だとすると、2/3になる。そして偶数の出る確率2/1と3/2を乗法すると3/1になる。
しかし、既に偶数が出た中でと条件づけて2/3としているのでそれにさらに2/1を乗じてしまうのはおかしいのだ。
また、上記のリンク先での計算では、Aという条件下でBという結果の出る確率を考える場合、Aという条件下でBの出る結果を全体からの確率判断をしている。
全体での4以上であれば4，5，6で1/2となるが、偶数下での4，6であり、それを全体で判断するので1/3となる。これを偶数下で判断すると3/2になる。
結果的には同じだが導出が違う。
1/3を1/2で割るので結果2/3となる。

条件付き確率の勘違い

何が言いたいかというと、Aという条件下で起こった確率とその条件下でBという事象が起こる確率は単に乗法すればいいと思っていたが、同時確率と条件つき確率を混同していたようだ。
同時確率　乗法定理
条件付き確率はAという条件下での発生確率をもとにしてBという結果が発生した場合のその発生確率を言っているので乗法定理ではない。

ベイズの定理を分かりやすく分解

B×A/B ＝ A×B/A　×　A　/ B

Bが起こった時にAが起こる確率（条件付確率）　＝　Aが起こった時にBが起こる確率（条件付確率）　×　Aが起こる確率　÷　Bが起こる確率

条件付確率＝同時確率/A又はB　※算出したい確率がAならBで割り、算出したい確率がBならAで割る

ジョーカー抜きのトランプからカードを1枚引く　
ハートであることをA　絵札であることをB　とする
A＝４分の１　B＝13分の3

Bが起こった時にAが出る確率＝52分の3　÷　4分の１　×　4分の1　÷　13分の3

モンティホール問題をベイズの定理を使って解く場合は
司会者がドアを開ける　→　解答者のドアに賞金がある　＝　解答者のドア　→　司会者ドア　×　解答者ドア　÷　司会者ドア
司会者がドアを開ける　→　残りのドアに賞金がある　＝　残りのドア　→　司会者ドア　×　残りのドア　÷　司会者ドア
　
この場合条件付確率と言っても同時確率にする必要はないが、　解答者のドアに賞金が入っていた場合に開けるドアの確率、　残りのドアに賞金が入っている場合に開けるドアの確率は結局自分で出す

 - 素朴な疑問 素朴な疑問